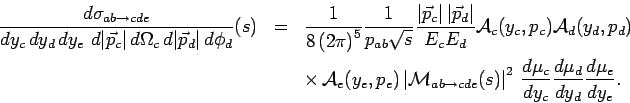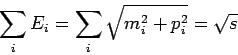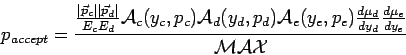|
|




Next: Medium Corrections
Up: Final State Decisions
Previous: Two body final states
Contents
Three body final states :
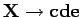 in the vacuum in the vacuum
In analogy to the two-particle final and utilizing equation (1.7)
and the variable transformation
we get
Hence we need to choose
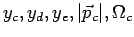 and and  independent of each other. The limits for the independent of each other. The limits for the 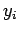 are given by the smallest and largest possible masses. The absolute values of the momenta are given by the smallest and largest possible masses. The absolute values of the momenta  are limited by the energy conservation. Evaluated in CM-System are limited by the energy conservation. Evaluated in CM-System
this demand sets the limits to
The value of 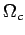 is choosen by choosing is choosen by choosing
![$\cos(\theta)\in[-1,1]$](img149.png) and and
![$\phi\in[0,2\pi]$](img150.png) by random. Once we have chosen those parameters, the full kinematics is fixed. Having choosen the parameters according to flat distribution we can define a probability to accept such a configuration by by random. Once we have chosen those parameters, the full kinematics is fixed. Having choosen the parameters according to flat distribution we can define a probability to accept such a configuration by
where 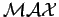 is chosen such that it is larger than the maximum of the nominator. With a Monte-Carlo decision we now accept or reject this configuration. We evaluate different configurations until we get one, which is accepted. is chosen such that it is larger than the maximum of the nominator. With a Monte-Carlo decision we now accept or reject this configuration. We evaluate different configurations until we get one, which is accepted.




Next: Medium Corrections
Up: Final State Decisions
Previous: Two body final states
Contents
Oliver Buss
2005-03-16
|

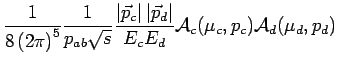
![\begin{displaymath}
y_i(\mu_i)=2\,\arctan\left[2\,\frac{\mu_i-M_i^0}{\Gamma^0_i}\right]; i\in\left\lbrace c,d\right\rbrace
\end{displaymath}](img126.png)