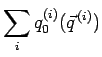Medium Corrections

GiBUU

Next: Place of production Up: Final State Decisions Previous: Three body final states Contents

Medium Corrections

In the medium we have a more complicated dispersion relation. Therefore also the phase space factors differ from the ones used above. Already in [Eff99] possibilities to implement the right phase-space factors were discussed. We will retreat to standard implementation. In a nutshell this prescription works the following:

Evaluate $s_{vacuum}$ .
Do the final state decision with vacuum kinematics assuming $s=s_{vacuum}$ .
Correct the final state by scaling the final state momenta by a factor in the CM frame.

The last point needs special discussion. Therefore we go to the CM-frame of the final state. Here energy and momentum conservation in step 2 result in a solution for the momenta $\vec{p}(i)$ which obeys

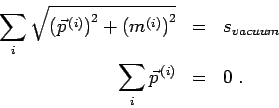$\begin{eqnarray*} \sum_i \sqrt{\left(\vec{p}^{\, (i)}\right)^2+\left(m^{(i)}\right)^2}&=&s_{vacuum} \\ \sum_i \vec{p}^{\, (i)}&=&0 \ . \end{eqnarray*}$

Now we want to define the four momenta in the medium. Let them be denoted by $q_{\mu}(i)$ . In the medium momentum and energy conservation demand

$\displaystyle \sum_i q_0^{(i)}(\vec{q}^{\, (i)})$	$\textstyle =$	$\displaystyle s$	(2.16)
$\displaystyle \sum_i \vec{q}^{\, (i)}$	$\textstyle =$	$\displaystyle 0 \ .$	(2.17)

The zeroth components $q_0^{(i)}$ are due to the potentials highly non-trivial functions of the vector components $\vec{q}^{\, (i)}$ . Hence our recipe is the following: Using the vacuum result for $\vec{p}^{\, (i)}$ we choose

$\begin{displaymath} \vec{q}^{\, (i)}= x\, \vec{p}^{\, (i)} \, \forall \, i \end{displaymath}$

where the scaling factor

is fixed by equation (2.16). Since all momenta are scaled by the same factor, the momentum conservation is fulfilled trivially.

Next: Place of production Up: Final State Decisions Previous: Three body final states Contents

Oliver Buss 2005-03-16