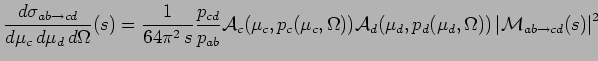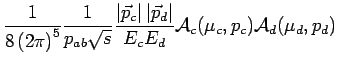|
|




Next: Medium modifications
Up: Reactions: Theoretical framework
Previous: The cross section for
Contents
The general definition of the cross section is given by (e. g. [H+02])
 |
|
|
(1.5) |
where denotes the n-particle phase space of the final-state particles,
 stands for the symmetry factor of the final state and stands for the symmetry factor of the final state and
represents the flux factor of the particles 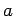 and and  . This flux factor can be expressed in the center of mass system by . This flux factor can be expressed in the center of mass system by
with the CM-momentum 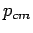 of the particles of the particles 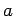 and and  .
In [Leh03]1.2 it was shown that one can express the cross section for the production of unstable particles .
In [Leh03]1.2 it was shown that one can express the cross section for the production of unstable particles 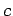 and and 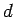 in the final state by in the final state by
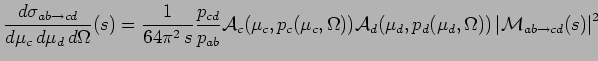 |
|
|
(1.6) |
with 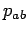 and and 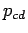 denoting the CM momenta of the denoting the CM momenta of the 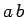 and the and the 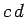 -system. Here one needs to assume that the Matrix element is only dependend on -system. Here one needs to assume that the Matrix element is only dependend on 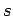 . The spectral functions depend only in the medium, which explicitly breaks Lorentz-invariance, on the four-momenta of the particles. Considering the vacuum-case they will only depend on the squares . The spectral functions depend only in the medium, which explicitly breaks Lorentz-invariance, on the four-momenta of the particles. Considering the vacuum-case they will only depend on the squares
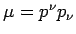 . .
For a three-particle final state one gets a more complicated result due to a rising number of degrees of freedom in the final state
Here 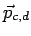 denote the CM-momenta of the particles c and d. The CM-momentum of denote the CM-momenta of the particles c and d. The CM-momentum of 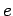 is given by total momentum conservation is given by total momentum conservation
Subsections




Next: Medium modifications
Up: Reactions: Theoretical framework
Previous: The cross section for
Contents
Oliver Buss
2005-03-16
|