Medium modifications

GiBUU

Next: Reactions: Numerical Implementation Up: Reactions of the type Previous: Reactions of the type Contents

Medium modifications

All the cross sections which we will later on utilize are so-called vacuum cross-sections. This refers to the fact that they are either measured in elementary processes or there value is determined in calculations which did not take any potentials into account. In the vacuum the dispersion relation is given by

$\begin{displaymath} p_{0}=\sqrt{\vec{p}^2+m^2} \ . \end{displaymath}$

Therefore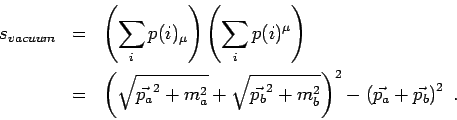

$\begin{eqnarray*} s_{vacuum}&=&\left(\sum_{i} p(i)_{\mu}\right) \left(\sum_{i} p... ...ec{p_b}^2+m_b^2}\right)^2-\left(\vec{p_a}+\vec{p_b}\right)^2 \ . \end{eqnarray*}$

Hence, all vacuum cross-sections are parameterized in terms of 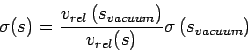$s_{vacuum}$ which usually differs from the real Mandelstam

in the medium. To take this into account we define

$\begin{displaymath} \sigma(s)=\frac{v_{rel}\left(s_{vacuum}\right)}{v_{rel}(s)} \sigma\left({s_{vacuum}}\right) \end{displaymath}$

where we implemented a flux factor correction as in the case of resonance production in equation (1.4). For the definition of $s_{vacuum}$ we choose the CM-frame of both particles as a prefered frame of reference. Therefore we boost with the full kinematics to this frame and evaluate there $s_{vacuum}$ .

Oliver Buss 2005-03-16