|
Next: Three body final states Up: Final State Decisions Previous: Resonance Production Contents
Here we need to utilize a Monte-Carlo description to choose the final state. In equation (1.6) we have seen that the two-particle final state depends both on the masses of the outgoing particles and their directions of motion. The Mandelstam |
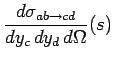 |
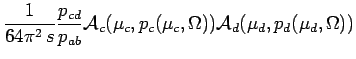 |
||
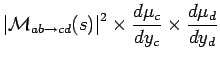 |
(2.14) |
with
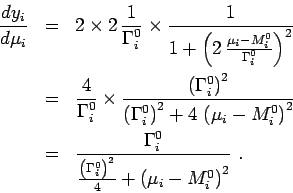
Now we choose
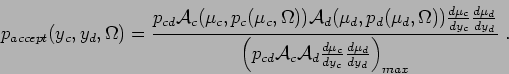
The denoted by
 is actually hard to find. We parametrize this maximal value by
is actually hard to find. We parametrize this maximal value by

The dimensionless factor
Next: Three body final states Up: Final State Decisions Previous: Resonance Production Contents Oliver Buss 2005-03-16
![\begin{displaymath}
y_i(\mu_i)=2\,\arctan\left[2\,\frac{\mu_i-M_i^0}{\Gamma^0_i}\right]; i\in\left\lbrace c,d\right\rbrace
\end{displaymath}](img126.png)