The cross section for a b R in the vacuum

GiBUU

Next: The cross section for Up: Resonance production: Previous: The mass of the Contents

The cross section for a b $\longrightarrow$ R in the vacuum

The cross section for $a\ b \rightarrow R$ in the vacuum is given by

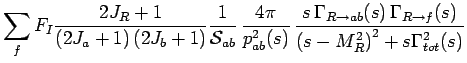$\displaystyle \sigma_{a\,b \rightarrow R}(s)$	$\textstyle =$	$\displaystyle \sum_{f} F_{I} \frac{2J_R+1}{\left(2J_a+1\right)\left(2J_b+1\righ... ...}(s) \, \Gamma_{R \rightarrow f}(s)}{\left(s-M_R^2\right)^2+s\Gamma_{tot}^2(s)}$
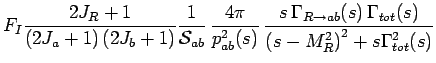	$\textstyle =$	$\displaystyle F_{I} \frac{2J_R+1}{\left(2J_a+1\right)\left(2J_b+1\right)} \frac... ...ghtarrow a b}(s) \, \Gamma_{tot}(s)}{\left(s-M_R^2\right)^2+s\Gamma_{tot}^2(s)}$	(1.2)

with

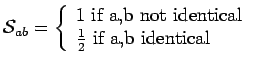$\displaystyle \mathcal{S}_{ab}=\left\lbrace \begin{array}{ll} 1 \mbox{ if a,b not identical} \\ \frac{1}{2} \mbox{ if a,b identical} \end{array}\right.$

(1.3)

being the symmetry factor of

and

and $p_{ab}$ , being the center of mass momentum of particles

and

, the

's define the total spin of the particles and

$\begin{displaymath} F_I=\left\langle I^a\, I^b ; i_z^a\, i_z^b \vert I^R\, i_z^a+i_z^b \right\rangle^{2} \end{displaymath}$

incorporates the Clebsch-Gordan coefficients due to Isospin.

Oliver Buss 2005-03-16