The mass of the resonance

GiBUU

Next: The cross section for Up: Resonance production: Previous: Resonance production: Contents

The mass of the resonance

The problem is here, that we need to know the mass of the resonance. We wish that total energy and momentum is conserved. Therefore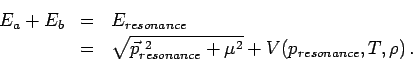

$\begin{eqnarray*} \vec{p}_{a}+\vec{p}_{b}&=&\vec{p}_{resonance} \end{eqnarray*}$

and

$\begin{eqnarray*} E_{a}+E_{b}&=&E_{resonance}\\ &=&\sqrt{\vec{p}^{\ 2}_{resonance}+\mu^2}+V(p_{resonance},T,\rho) \, . \end{eqnarray*}$

The mass $\mu$ of the resonance is therefore given by the energy of the incoming particles:

$\begin{displaymath} \mu=\left[\left(E_{resonance}-V(p_{resonance},T,\rho)\right)^2-\vec{p}^{\ 2}_{resonance}\right]^{\frac{1}{2}} \end{displaymath}$

(1.1)

This equation is only valid in the case that the potential is independend of the mass of the resonance. Note that equation (1.1) must be evaluated in the local rest frame, since only there the potential is well defined. This is a technical complication of the procedure, because one needs to boost all variables to this system.

Oliver Buss 2005-03-16