Xsections – Hepforge

GiBUU

Next: Up: Initial channel Previous: Contents

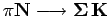
$\mathbf{\pi N \longrightarrow \Sigma \, K }$

As implemented in [Eff99] we use a parametrization according to Tsushima et al [THF97] for

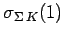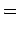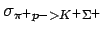$\displaystyle \sigma_{\Sigma K}(1)$	$\textstyle =$	$\displaystyle \sigma_{\pi^{+} p -> K^{+} \Sigma^{+}}$	(2.9)
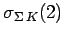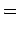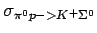$\displaystyle \sigma_{\Sigma K}(2)$	$\textstyle =$	$\displaystyle \sigma_{\pi^{0} p -> K^{+} \Sigma^0}$	(2.10)
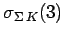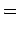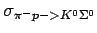$\displaystyle \sigma_{\Sigma K}(3)$	$\textstyle =$	$\displaystyle \sigma_{\pi^{-} p -> K^{0} \Sigma^0}$	(2.11)
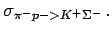$\displaystyle \sigma_{\Sigma K}(4)$	$\textstyle =$	$\displaystyle \sigma_{\pi^{-} p -> K^{+} \Sigma^-} .$	(2.12)

Assuming isospin symmetry and assuming that everything goes through an 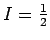$I=\frac{1}{2}$ resonance, we get

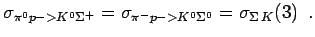$\displaystyle \sigma_{\pi^{0} p -> K^{0} \Sigma^+}= \sigma_{\pi^{-} p -> K^{0} \Sigma^0}=\sigma_{\Sigma \, K}(3) \,\ .$

(2.13)

These last five cross sections (2.9) to (2.13) define all possible channels with a proton in the initial state. Channels with an initial neutron are defined by charge conjugation:

$\begin{eqnarray*} \sigma_{\pi^{-} n -> K^{0} \Sigma^{-}} &=\sigma_{\pi^{+} p -> ... ...igma_{\pi^{-} p -> K^{0} \Sigma^0}&=\sigma_{\Sigma \, K}(3) \, . \end{eqnarray*}$

Oliver Buss 2005-03-16